Electronic Structure

Diabatic States for Electron and Energy Transfer

While electronic structure has proved remarkable successful in recent years at constructing adiabatic electronic eigenstates for ever larger molecules, these techniques always assume frozen nuclei. When nuclear-electronic coupling is non-negligible, however, these adiabatic electronic states are not necessarily stable. A classic example would be Fe+2/Fe+3 complexes, where the adiabatic states predict complete charge delocalization over the two metal centers. It is known, of course, that charge does localize and, as such, the adiabatic eigenstates are not stable or meta-stable in solution. We have recently developed tools that calculate diabatic states by "localizing" a set of adiabatic eigenstates, much in the same spirit as quantum chemistry has localized orbitals for the past 50 years (since Ruedenberg's famous 1963 paper.) Using these localized states as guesses for the initial and final states of electron and energy transfer processes, we have already modeled some nonequilibirum processes very accurately within the context of Marcus theory. Work is ongoing for how to find the optimal diabatization method and how to best integrate these methods with electronic structure theory. We have shown that these methods produce diabatic states with very small derivative couplings.


12. Subotnik, Yeganeh, Cave and Ratner. Constructing Diabatic States from Adiabatic States: Extending Generalized Mulliken Hush to Multiple Charge Centers with Boys Localization J. Chem. Phys. 129, 244101 (2008) [PDF] | TYPO's-[pdf]

16. Subotnik, Cave, Steele and Shenvi. The Initial and Final States of Electron and Energy Transfer Processes: Diabatic States as Motivated by System-Solvent Interactions J. Chem. Phys. 130, 234102 (2009) [PDF] | TYPO's-[pdf]

33. Fatehi, Alguire, and Subotnik. Derivative couplings and analytic gradients for diabatic states, with an implementation for Boys-localized configuration-interaction singles. J. Chem. Phys. 139, 124112 (2013) [PDF] | TYPO's-[pdf]




Accurate Excited State Energies

Calculating ground state energies is standard practice in the world of quantum chemistry, but calculating excited state energies is far more difficult. In particular, one requires a reasonably high degree of accuracy if one wants to accumulate the correct ordering of excited states, and also obtain the correct geometries for excited state crossings. Our efforts at generating accurate excited state energies have been based upon the idea of adding "post CIS" corrections for electron-electron correlation. In particular, we are guided by the principle of adding doubles corrections on top of CIS wavefunctions. Thus far, we have had some successes, but challenges do remain in balancing the energies of charge transfer states, locally excited states, Rydberg states, and the ground state.




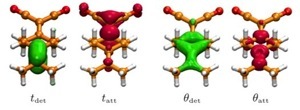
32. Liu, Ou, Alguire and Subotnik. Communication: An inexpensive, variational, almost black-box, almost size- consistent correction to configuration interaction singles for valence excited states. J. Chem. Phys, 138, 221105 (2013) [PDF]

38. Liu and Subotnik. The Variationally Orbital-Adapted Configuration Interaction Singles (VOA-CIS) Approach to Electronically Excited States. [PDF]




Derivative Couplings and TD-DFT

From the perspective of standard, adiabatic quantum chemistry, all non-Born Oppenheimer effects are incorporated in the so-called derivative couplings. One of our group's research interests is the construction of derivative couplings between excited states, where we have found several interesting themes (and many more still exist).

  • One of our accomplishments has been to understand the role of translational variance of derivative couplings. Translational variance arises because the Born-Oppenheimer electronic states are real (and, thus, not moving with nuclei). One can show that, in a moving frame, these effects go away to zeroth order, and that all non-Hermitian matrix elements that arise should be discarded.

    • 26. Fatehi, Alguire, Shao and Subotnik. Analytical Derivative Couplings Between Configuration Interaction Singles States with Built-in Translation Factors for Translational Invariance
    J. Chem. Phys. 135, 234105 (2011) [PDF] Link


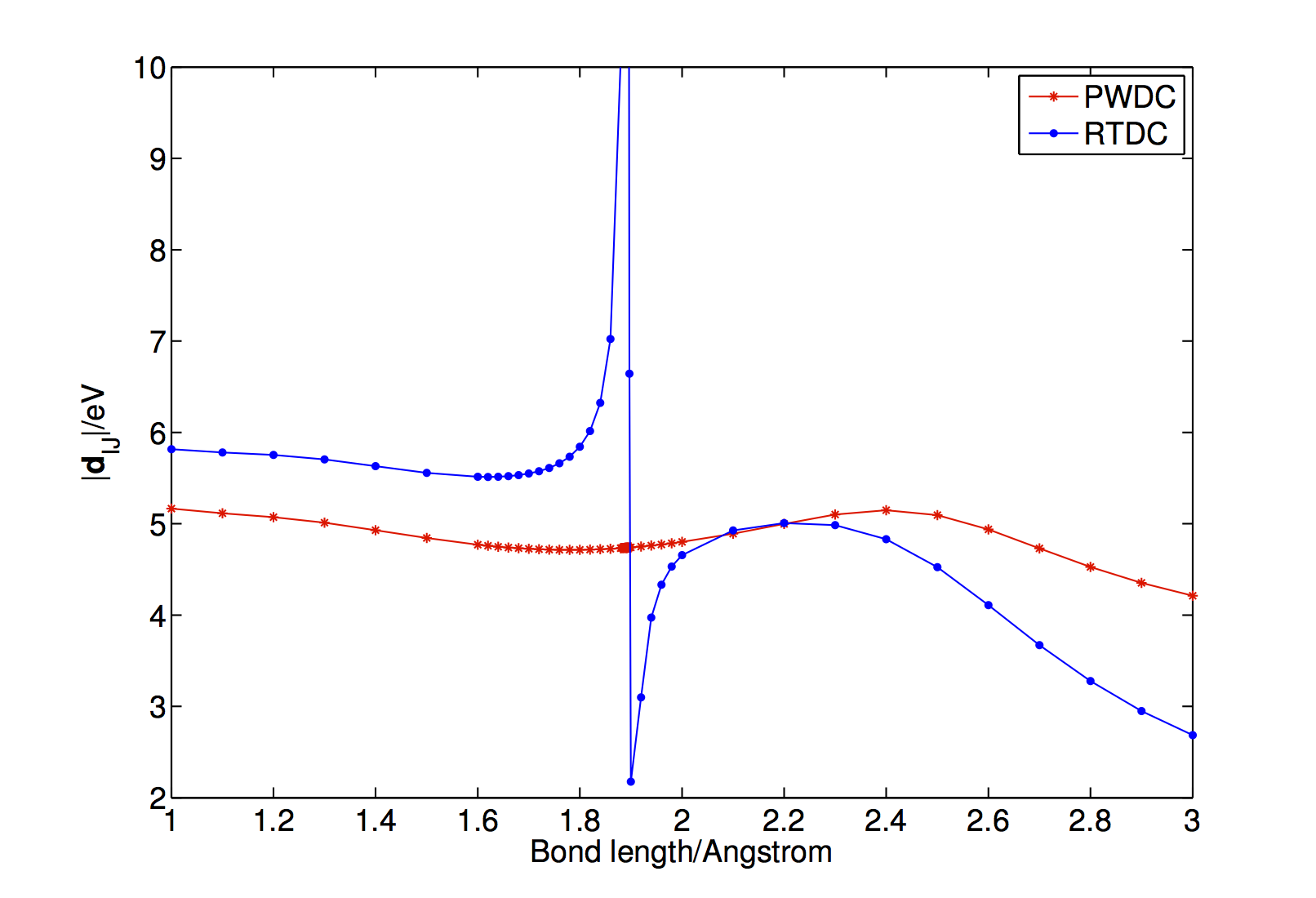
  • In the context of TD-DFT, derivative couplings become complicated to construct because there is no formal wavefunction in reponse theory. That being said, one can either (i) construct pseudo-wavefunctions for RPA states or (ii) use formal response theory to construct derivative couplings. Either way, one arrives at very similar expressions. However, with formal response theory, one finds spurious poles that are not physical. Research into these derivative couplings is ongoing.


  • 43. Alguire, Ou, and Subotnik. "Calculating Derivative Couplings between Time-Dependent Hartreeāˆ’Fock Excited States with Pseudo-Wavefunctions"
    J. Phys. Chem. B 119, 7140-7149 (2015) [PDF]       link


  • 44. Ou, Alguire, and Subotnik. "Derivative Couplings between Time-Dependent Density Functional Theory Excited States in the Random-Phase Approximation Based on Pseudo-Wavefunctions: Behavior around Conical Intersections."
    J. Phys. Chem. B 119, 7150-7161 (2015) [PDF]       link

  • 52. Q. Ou, G. D. Bellchambers, F. Furche, and J. E. Subotnik. "First order derivative couplings between excited states from adiabatic TDDFT response theory."
    J. Chem. Phys. 142 064114 (2015) [PDF] Link