Surface Hopping Near Metal Surfaces

When molecules approach metal surfaces, the normal rules of nonadiabatic dynamics become unclear. Now, rather than just a handful of electronic states, there is a continuum of electronic states. As such, standard surface hopping with a set of (infinitely many) adiabatic states is unrealistic. Instead, two different approaches have been proposed:

  • One can work with a surface-hopping perspective, whereby there is no energy conservation. This can actually be derived from Redfield theory and is valid in the limit of our sphere electrochemistry.
  • One can work with a ground-state mean-field perspective, whereby electronic transitions become a form of "electronic friction". The picture of electronic friction is an old (but slightly confusing!) concept that should be valid in the limit of our sphere electrochemistry.

    • In a series of recent articles, we have examined both approaches and shown how to connect these different models into a universal theory (this is now being tested). The theory of molecular dynamics near metal surfaces is one of our key current research interests.






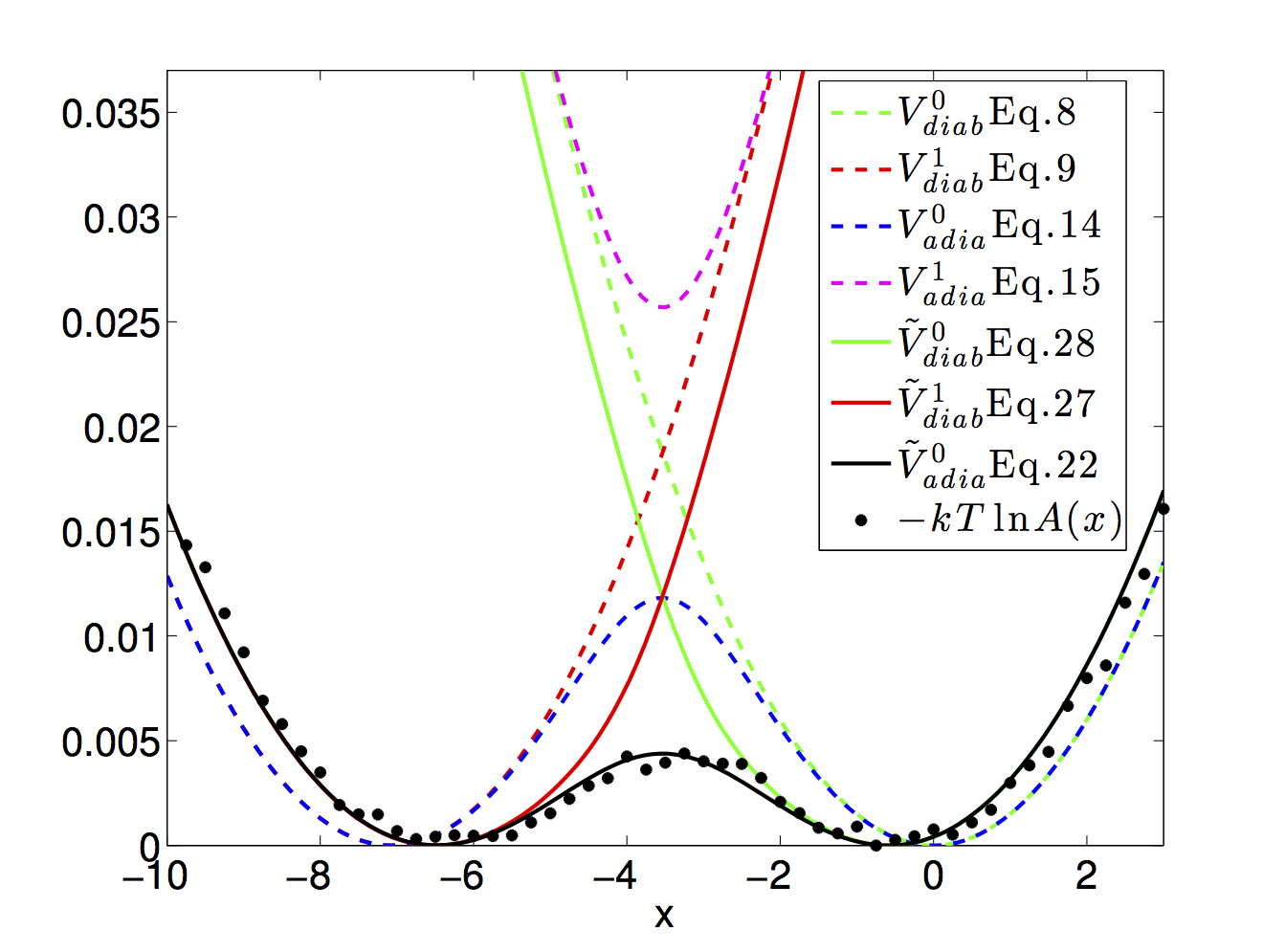
    58. W. Dou, A. Nitzan, and J.E. Subotnik. "Frictional effects near a metal surfaces."
    J. Chem. Phys. 143, 054103 (2015) [PDF]       link


    Electronic Friction

    One of our most important results has been to establish a universal, Markovian electronic friction tensor that unified and extended the works ofSuhl, Head-Gordon and Tully, von Oppen, Brandbyge et al, Persson and Persson, Hynes, Galperin, and others and produced a final expression that was valid in and out of equilibrium, with our without electron-electron interactions (though of course only in the limit of slow nuclear motion.) In the figure below, you can see the electronic friction model in the presence of electro-electron interactions in the limit of the Kondo resonance, where very interesting features appear. < br>






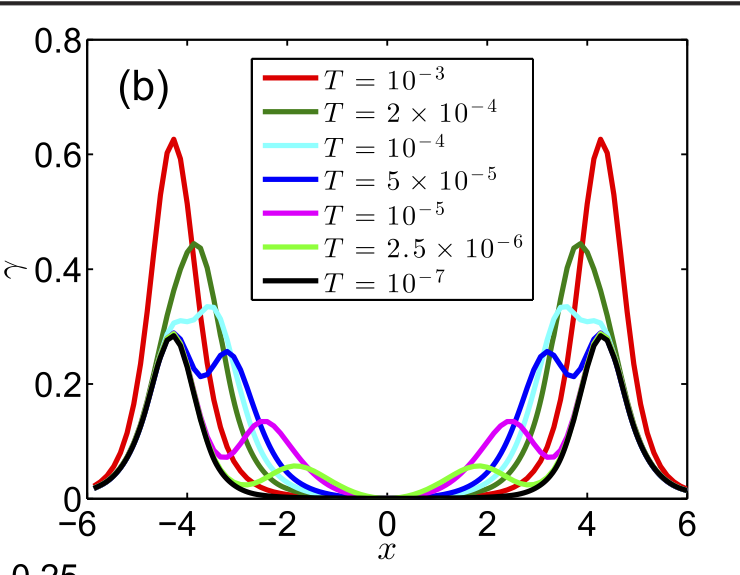
    77. W. Dou, G. Miao, and J. E. Subotnik. "Born-Oppenheimer Dynamics, Electronic Friction, and the Inclusion of Electron-Electron Interactions"
    Phys. Rev. Lett. 119, 046001 (2017) [PDF]     [Supplementary Info]       link









    Software for modeling CV curves

    Cyclic voltammetry (CV) is a crucial technique within the real of electrochemistry for measuring the dynamics of charge transfer reactions at metal surfaces. Within a typical CV measurement, one ramps up an electric field to drive reactants towards a metal surface where (for a Faradaic event), a charge transfer event occurs. Thus, as far as modeling CV curves, there are two key time scales of interest: 1. the diffusion time for charged particles and 2. the time scale for electron transfer. One can partially probe these time scales by ramping up the voltage slowly (the 'reversible' regime) or quickly (the 'irreversible' regime).

    As far as modeling these processes, for the most part (and who knows why), this task usually is left to chemical engineers. There are a few propriety executables that one can download. The math describing CV curves is complicated because the time scale for diffusion is usually much longer than the time scale for electron transfer, such that solving the relevant partial different equations (PDEs) is stiff; special care must be taken when doing integration. The usual approach is to simulate a grid in real space, propagate diffusion over such a grid, and invoke the relevant boundary equation for simulating electron transfer. This approach works very well but makes modeling absorption difficult.

    In collaboration with   Jianfeng Lu (Duke University), we have now implemented a grid-free Green's function approach for simulating CV curves that can treat absorption, as well as Marcus-Hush and Butler-Volmer dynamics.




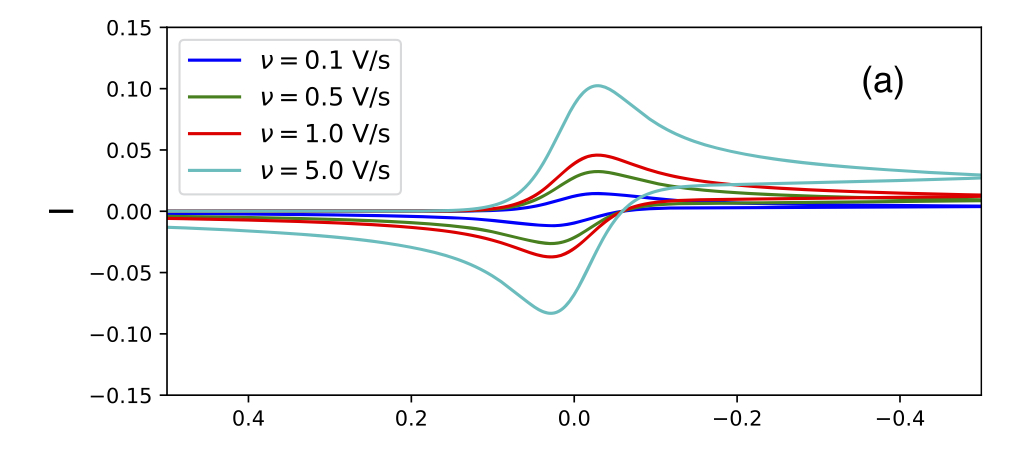
    124. A.J. Coffman, J. Lu, J.E. Subotnik. "A grid-free approach for simulating sweep and cyclic voltammetry"
    J. Chem. Phys. 154, 161101 (2021) [PDF]           link        





    Download a GUI for our grid-free (python) CV code here: GUI pyCV Authors: Alec Coffman, Sam May. In order to execute, you might need to download Anacaonda and then run "python pycv_may24_2022.py"