Spectroscopy
Semiclassical Light-Matter Dynamics
Within the theoretical chemistry community, we usually worry more about molecules/materials than about photon fields. For the most part, we consider classical (as opposed to quantum) electromagnetic fields, and we use perturbation theory to express electromagnetic signals as a function of correlation functions of molecular. And yet this perspective is limiting for two reasons. First, if one cannot visualize EM fields, one cannot build intuition for coupling the Schrodinger equation to the Maxwell equations.
Second, in the context of modern plasmonics, because nanostructures are so much larger than molecules with such stronger absorption cross-sections, light-matter interactions are no longer perturbative always. Thus, there is a need to go beyond traditional dynamics approaches.
Furthermore, there is reason to think that we can make progress here: there has been a ton of work done in the area of coupled nuclear-electronic dynamics over the years, but far less has been done in the arena of coupled electron-photon dynamics. Modeling EM fields has historically been the perview of the quantum optics community, where little attention has focused on the matter side of things. One interesting result that has already arisen: when you mix quantum electrons and classical light, you cannot recover electron-electron correlations while also obeying causality. The world of semiclassical theory has many surprises in store for us when we turn to light-matter interactions.
With this background in mind, one of the main questions that we are asking nowadays in the context of light-matter interactions is this: What is the most natural semiclassical approach for modeling electronic transitions and electromagnetic (EM) fields explicitly at the same time?
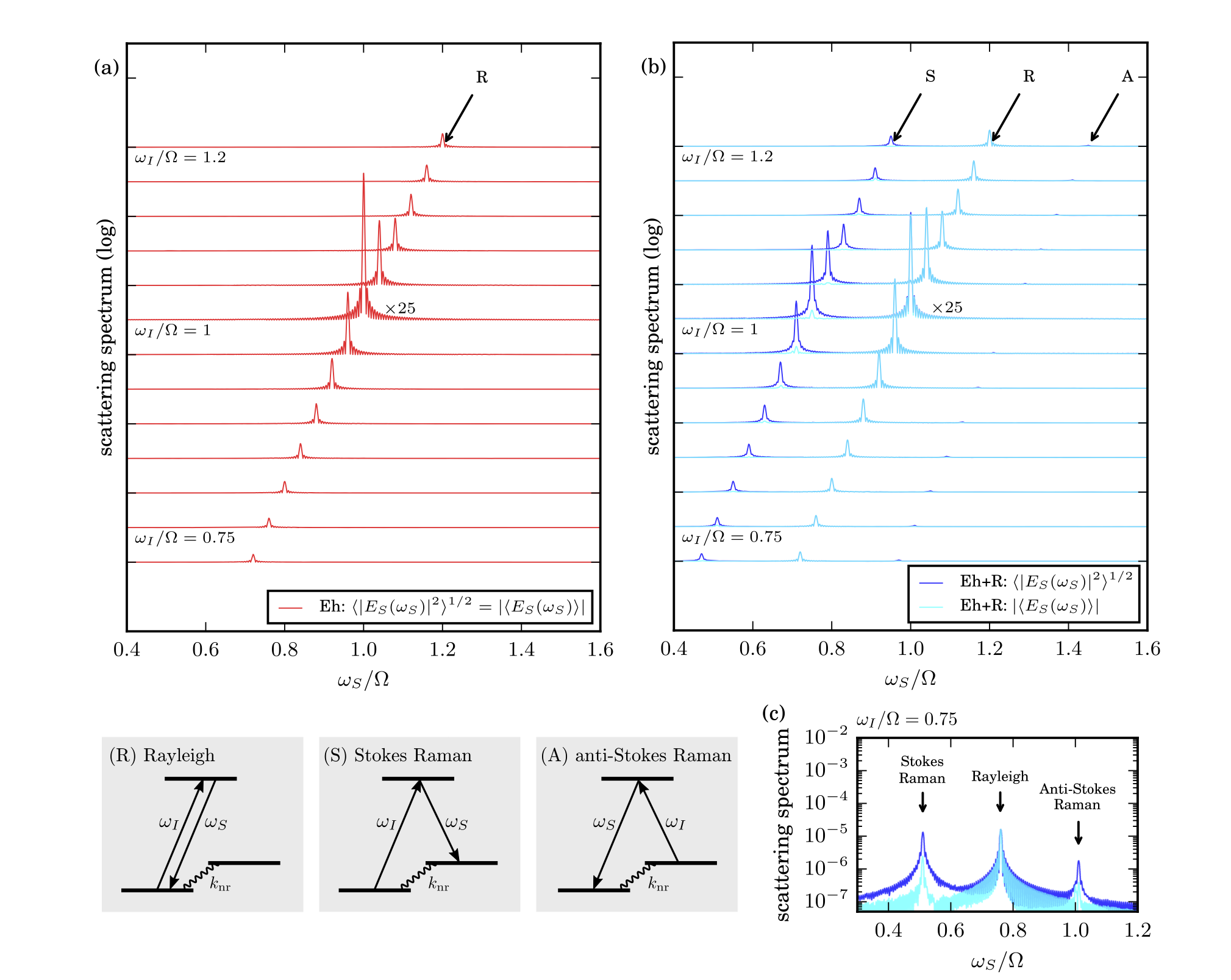
A naive, Ehrenfest merger of the Liouville equation with Maxwell's equations does not recapitulate spontaneous emission: can we do better? To that end, we are now structuring a new dynamics approach (``Ehrenfest+R'')
to do just that: to improve upon Ehrenfest dynamics by incorporating vacuum fluctuations and putting in spontaneous emission. The preliminary results are looking very good so far.
Papers
93. H.-T. Chen, T. E. Li, M. Sukharev. A. Nitzan, J. E. Subotnik "Ehrenfest+R dynamics. II. A semiclassical
QED framework for Raman scattering"
J. Chem. Phys.
150, 044103 (2019)
[PDF]
link
Polaritonics
Semiclassical Light-Matter Dynamics
In recent years, there has been a explosion of interesting in polaritonics, the field of science associated with molecules interacting collectively with a small number of radiation modes inside of a cavity. In particular, one fascinating question has emerged: If molecules interact collectively with one radiation mode and this interaction leads to a splitting of the radiation mode as observed spectroscopically through a Rabi splitting, does that mean that there will be a collective effect on the molecular motion? In other words, if molecule A feels molecules B,C, D, ... etc enough such that the transmission through a cavity depends on the collective number of molecules in the cavity, does that mean that molecule A's propensity to undergo a reaction will depend also on the number of molecules in the cavity?
This question is now being pondered both for excited state and ground state properties, as several recent experiments have been published. Unfortunately, from a computational/theoretical point of view, answering these questions is difficult because ab initio quantum methods are wildly too expensive and so most calculations end up using very parameterized Hamiltonians, often with unrealistic parameter sets. Our approach has been to make the compromise whereby we give up on quantum dynamics and run everything classically (with a classical cavity mode). The resulting CavMD code interfaces well with normal MD - there is not just one more degree of freedom.
What have we found? Although we have found no evidence of any ground state effects, we have found evidence of interesting excited state effects, whereby a highly exicted polariton can dump its energy into the vibrational energy of a single molecule if the energy levels are lined up correctly. We predict this effect will be observed soon. This effect cannot be observed with a model Hamiltonian with quadratic harmonic oscillators; the anharmnonic nature of vibrations according to an atomistic force field plays a crucial role here.
 Papers
Papers
139. T.E. Li, A. Nitzan, J.E. Subotnik "Energy-efficient pathway for selectively exciting solute molecules to high vibrational states via solvent vibration-polariton pumping"
Nat. Comm
13, 1 (2022)
link